广州有道有限元培训学校_ANSYS残余应力分析应用

本文建立了薄板焊接有限元模型，采用高斯热源并利用ansys软件对焊接过程做了模拟。计算表明，焊接后的较大的残余应力分布在焊缝处，这为实际的焊接过程控制提供了一定的指导。

1 引言
焊接结构一个很明显的特点是有较大的焊接应力和变形。由于焊接生产中，绝大部分焊接方法都采用局部加热，所以不可避免地将产生焊接应力和变形。焊接应力和变形不但可能引起热裂纹、冷裂纹、脆性断裂等工艺缺陷，而且在一定条件下将影响结构的承载能力，如强度，刚度和受压稳定性。除此以外还将影响到结构的加工精度和尺寸稳定性。以往，对焊接温度场、应力和变形的分析都是通过实验的方法测量并采集数据，进行定量的分析。由于受实验各方面的限制，所得数据的精确度并不高而且浪费大量的人力、物力和时间。虽然这类问题可通过解析方法，求解某些特定的微分方程组来进行定量计算，然而，只有在十分简单的情况下并且作许多简化的假设，才有可能求得这些方程闭和的解析解。而实际的焊接问题多种多样，边界条件十分复杂，用解析方法来求解这类微分方程是十分困难的。在高速电子计算机发展的今天，大多采用数值模拟的方法。因此，在设计和施工时充分考虑焊接应力和变形这一特点是十分重要的。可见，对焊接应力和变形进行计算和分析有很重要的现实意义。
本文针对低碳钢薄板焊接时，应用高斯分布热源模型，建立了三维薄板堆焊的温度场有限元数值分析模型，并以此为基础考虑了材料的非线性采用热弹塑性有限单元法，得到了薄板的焊接过程的瞬态温度场、瞬态热应力和残余应力。
2 焊接模拟相关理论
2.1 非线性热传导分析的基本原理
焊接是一个局部加热到高温，并随后冷却的过程。随着热源的移动，整个焊件的温度随时间和空间急剧变化，材料的热物理性能也随温度剧烈变化，同时还存在熔化和相变时的潜热现象。因此，焊接温度场分析属于典型的非线性瞬态热传导问题。
非线性瞬态热传导问题的控制方程为:

        (1)
式中: c为材料比热容; ρ为材料密度; λ为导热系数;T为温度场分布函数; Q为内热源; t为传热时间。这些参数中c、ρ、λ都随温度变化。
焊接温度场的计算通常用到以下两类边界条件:
1)己知边界上的热流密度分布
2)己知边界上的物体与周围介质间的热交换
2.2 非线性瞬态热传导的有限元分析
由于焊接温度场的分析是典型的非线性瞬态热传导问题，而这类问题的求解特点是在空间域内用有限单元网格划分，而在时间域内则用有限差分网格划分。
瞬态传热过程是指一个系统的加热或冷却过程。在这个过程中系统的温度、热流率、热边界条件以及系统内能随时间都有明显变化。根据能量守恒原理，瞬态热平衡可以表达为（以矩阵形式表示）：
        (2)
式中：为传导矩阵，包含热系数、对流系数及辐射和形状系数；
    [K]为比热矩阵，考虑系统内能的增加；
    [C]为节点温度向量；
    [T]为温度对时间的导数；
    [T]为节点热流率向量，包括热生成；
    {Q}因为焊接过程中材料热性能随温度变化，如K(T)，C(T)等；边界条件随温度变化，如h(T)等；含有非线性单元；考虑辐射传热；非线性热分析的热平衡方程为：
        (3)
2.3 焊接应力和变形的分析理论
由于高度集中的瞬时热输入，在焊接过程中和焊后将产生相当大的焊接应力和变形。焊接应力和变形计算是以焊接温度场的分析为基础，同时考虑焊接区组织转变对应力应变场带来的影响。热弹塑性分析是在焊接热循环过程中通过一步步跟踪热应变行为来计算热应力和应变的，该方法需要采用有限元计算方法在计算机上实现采用这种方法可以详尽地掌握焊接应力和变形的产生及发展过程。随着大型有限元软件的开发并取得了良好的效果，这种方法被越来越多的学者采用。本文也是基于此理论，借助于有限元软件在计算机上实现对焊接应力和变形的模拟研究的。
2.3.1 热弹塑性分析的特点和假定
热弹塑性问题是一个热力学问题。作为热力学系统的焊接材料，其自由能密度不仅与应变有关，而且还与温度有关。也就是说，力学平衡方程中有与温度有关的项。从能量上看，输入的热能在使焊接材料温度上升的同时，还由于结构的膨胀变形做功而消耗一部分。这时，在热传导平衡方程中，要增加与应力有关的项。因此，严格的说，温度场与应力场是相互藕合的。这从图3-1和图3-2能很清楚的看到。*这种祸合效果除个别特殊情况外，一般都很小，而且焊缝附近的温度变化很大，材料的各种物理性能也相应变化很大，这种影响与上述耦合效应相比要大得多。所以就焊接的热弹塑性而言，取非祸合的应力场和温度场是合适的。
在热弹塑性分析时有如下一些假定:
(1)材料的屈服服从米赛斯(Von Mises)屈服准则;
(2)塑性区内的行为服从塑性流动准则和强化准则;
(3)弹性应变、塑性应变与温度应变是不可分的;
(4)与温度有关的力学性能、应力应变在微小的时间增量内线性变化。
2.3.2 屈服准则
屈服准则是一个可以用来与单轴测试的屈服应力相比较的应力状态的标量表示。因此，知道了应力状态和屈服准则，程序就能确定是否有塑性应变产生。在多轴应力状态下，屈服准则可以用下式来表示：
        (4)
其中σ_e为等效应力，σ_y为屈服应力。
当等效应力超过材料的屈服应力时，将会发生塑性变形。
Von Mises屈服准则是一个比较通用的屈服准则，尤其适用于金属材料。对于Von Mises屈服准则，其等效应力为：
        (5)
其中：σ₁，σ₂，σ₃为三个主应力
2.3.3 流动准则
流动准则描述了发生屈服时，塑性应变的方向，也就是说，流动准则定义了单个塑性应变分量（ε^pl_x，ε^pl_y等）随着屈服是怎样发展的。流动准则由以下方程给出：
        (6)
其中：λ是塑性乘子（决定了塑性应变量），Q为塑性势，是应力的函数（决定了塑性应变方向）。
一般来说，流动方程是塑性应变在垂直于屈服面的方向发展的屈服准则中推导出来的，即Q等于屈服函数，这种流动准则叫作关联流动准则，如果使用其它的流动准则（从其它不同的函数推导出来），则叫作不关联的流动准则。

2.3.4 强化准则
强化准则描述了初始屈服准则随着塑性应变的增加是怎样发展的。一般来说，屈服面的变化是以前应变历史的函数，在ANSYS程序中，使用了三种强化准则:等向强化，随动强化，混合强化。对于焊接问题一般采用等向强化，可以得到比较好的计算结果。
2.4 热源模型的选择
通常解析方法较简单，意义明确，容易计算，但由于其假设太多，难以提供在焊接热影响区的精确计算结果，而且考虑不到电弧力对熔池的冲击作用。采用有限元和有限差分法，应用高斯分布的表面热源分布函数计算，可以引入材料性能的非线性，可进一步提高高温区的准确性，但仍未考虑电弧挺度对熔池的影响。从球状、椭球到双椭球热源模型，每一种方案都比前一种更准确，但也伴随着计算量的增加，使这些热源分布函数更利于应用有限元法或差分法在计算机上进行计算，而且实践也证明能得出较满意的模拟结果。对于通常的焊接方法如手工电弧焊、钨极氢弧焊，采用高斯分布的函数就可以得到较满意的结果。对于电弧冲力效应较大的焊接方法，如熔化极氢弧焊和激光焊，常采用双椭球形分布函数。为求准确，还可将热源分成两部分，采用高斯分布的热源函数作为表面热源，焊件熔池部分采用双椭球形热源分布函数作为内热源。
本人采用高斯热源来模拟电弧，现将高斯热源简述如下：焊接时，电弧热源把热能传给焊件是通过一定的作用面积进行的，这个面积称为加热斑点。加热斑点上热量分布是不均匀的，中心多而边缘少。费里德曼将加热斑点上热流密度的分布近似地用高斯数学模型来描述，
距加热中心任一点A的热流密度可表示为如下形式:
        (7)
式中:q_m为加热斑点中心较大热流密度:R为电弧有效加热半径;r为A点离电弧加热斑点中心的距离。对于移动热源
        (8)
这种热源模型在用有限元分析方法计算焊接温度场时应用较多。在电弧挺度较小、对熔池冲击力较小的情况下，运用这种模型能得到较准确的计算结果。
2.5 潜热处理
焊接过程中，母材熔化时，由固态变为液态，要吸收能量，反之熔池凝固时由液态变成固态，要放出热量，所以在计算温度场时，要考虑熔池相变潜热对温度场的影响。否则计算结果会有较大偏差。对于固态相变，由于其潜热一般比固液相变潜热小很多，通常将其忽略。但在高强钢焊接时*考虑其影响。ANSYS在考虑潜热时引入焓，其数学表达式：
        (9)
3 建立模型和求解
模型尺寸为100×100×6，电弧在钢板中间沿直线运动，因此在计算时去模型的一半进行研究。其有限元模型如图1。本文采用间接法计算薄板的热应力问题，使用solid70进行热计算，使用solid45进行应力计算。为了增加计算精度在靠近焊缝10mm处采用加密网格，网格大小控制在1mm，在远离焊缝处采用较疏的网格。

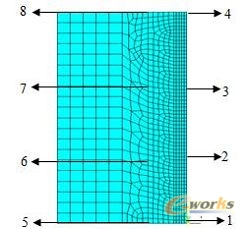
图1 平板焊接的有限元模型图2 有限元模型中考察的点

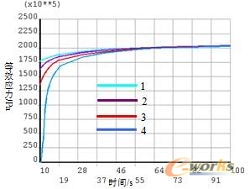
为了研究焊接过程中，薄板的温度场和应力场变化的规律，本文选取了图2所示的8个考察点1到4点为焊缝中心的点；5到8点为到焊缝一定距离的点。
焊接参数如下:
电弧电压U=15V;焊接电流I=1580A;焊接速度v=10m/s；焊接热效率η=0.6;电弧有效加热半径R=3E-3m。焊接材料为低碳钢其材料性能如表所示:

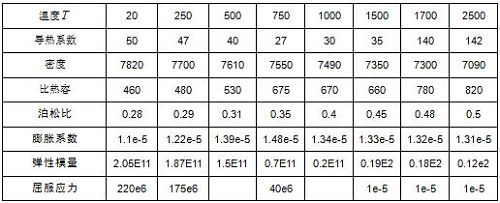
其热计算和应力计算结果如下：

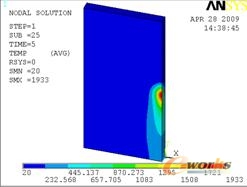
图3 0.2s时刻的温度场云图图4 5s时刻的温度场云图

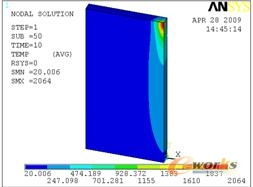
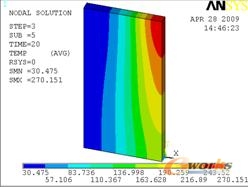
图5 10s时刻的温度场云图图6 20s时刻的温度场云图

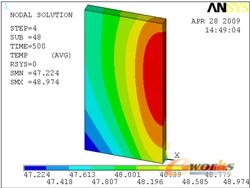
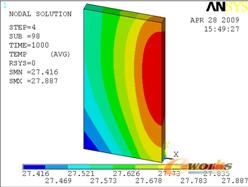
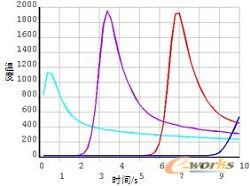
图3到图8给出了不同时刻的温度场云图，从图中可以看出焊接时间为10s，冷却时间为990s。在焊接过程中，焊接中心温度较高达到2100度，焊接完毕后温度从热源中心迅速向对点扩散，较高温度迅速下降，在20s时刻较高温度仅为270度左右，在500s时刻较高温度仅有48度，而且较高温度和较低温度相差仅1度说明薄板的温度场迅速达到一致。

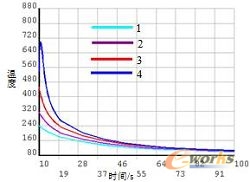
图7 500s时刻的温度场云图图8 1000s时刻的温度场云图

图9 1-4考察点的温度与时间的关系图10 1-4考察点的温度与时间的关系

图11 5-8考察点的温度与时间的关系图12 5-8考察点的温度与时间的关系

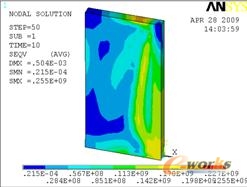
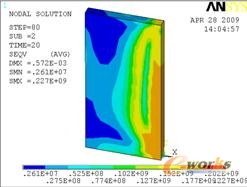
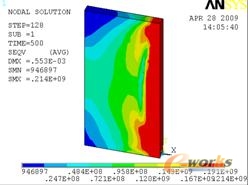
　　图9到12给出了8个考察点温度随时间变化的规律，由图9可以看出2点和3点在热源到来时温度迅速升高，而当热源离开后又迅速下降。从图10可以看出，焊缝中心处在100s时刻基本达到各处温度相同，并且随时间以相等速度下降。由图11和图12可知：在离焊缝一定距离处的四个点在前10s内都是稳定升温，直到大约20s左右才开始下降并且下降速度小于焊缝处的四个点这也是符合实际规律的。

图13 0.2s时刻的等效应力云图图14 5s时刻的等效应力云图

图15 10s时刻的等效应力云图图16 20s时刻的等效应力云图

图17 500s时刻的等效应力云图图18 1000s时刻的等效应力云图

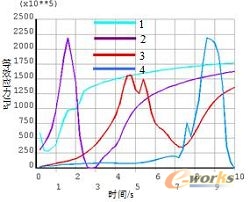
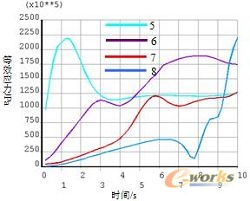
　　图13到图18给出了不同时刻薄板的热应力云图，由图13可知，在焊接开始时较大的热应力发生在热源处，从图14可知在焊接过程中的由于热源中心处的温度超过了金属溶点因此此处的应力为0即为溶池。这一定也是符合实际的。从图21和22可以看出，较后的残余应力的分布规律为焊缝出较大，两个角点较小，并且从焊缝到一边呈下降趋势。

图19到图22给出了8个考察点热应力与时间的关系图。由图19可知：焊缝处的四个点的热应力随时间变化都比较剧烈，尤其是2、3和4点处更是大起大落，在焊接结束后，焊缝处的热应力继续升高，直到一个稳定值并且这个稳定值四个点基本相同。从图21和22可以看出，5到8点在焊接过程中除了5点的热应力变化波动大，其他三个点都是升高趋势，在焊接结束后，四个点的热应力都在下降，且8点下降的较为明显。